Question:
In the given figure, PR =
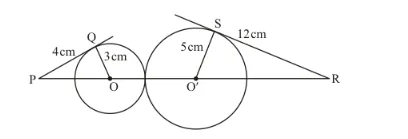
(a) 20 cm
(b) 26 cm
(c) 24 cm
(d) 28 cm
Solution:
We know that the radius will always be perpendicular to the tangent at the point of contact.
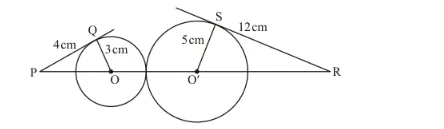
Therefore,
$O Q \perp O P$
Hence we have,
$O P^{2}=O Q^{2}+Q P^{2}$
$O P^{2}=4^{2}+3^{2}$
$O P^{2}=16+9$
$O P^{2}=25$
$O P=\sqrt{25}$
$O P=5$
Also,
OO’ = sum of the radii of the two circles
OO’ = 3 + 5
OO’ = 8
Since radius is perpendicular to the tangent, ![]() . Therefore,
. Therefore,
$O^{\prime} R^{2}=O^{\prime} S^{2}+S R^{2}$
$O^{\prime} R^{2}=12^{2}+5^{2}$
$O^{\prime} R^{2}=144+25$
$O^{\prime} R^{2}=169$
$O^{\prime} R=\sqrt{169}$
$O^{\prime} R=13$
PR = PO + OO’ + O’R
PR = 5 + 8 + 13
PR =26
Therefore, option (b) is correct.
