In the given figure, prove that

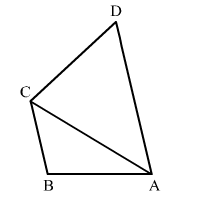
Solution:

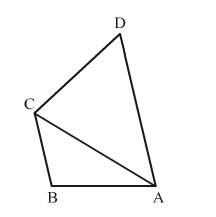
Given: Quadrilateral ABCD

To prove:
(i) CD + DA + AB > BC
(ii) CD + DA + AB + BC > 2AC

Proof:
(i)

In $\Delta A C D$,

$C D+D A>C A \quad \ldots(1)$

In $\Delta A B C$,

$A B+C A>B C \quad \ldots(2)$

Adding $(1)$ and $(2)$, we get

$C D+D A+A B+C A>C A+B C$

$\therefore A B+C D+D A>B C$

(ii)

In $\Delta C D A$

$C D+D A>C A \quad \ldots(3)$

In $\Delta B C A$,

$B C+A B>C A \quad \ldots(4)$

Adding $(3)$ and $(4)$, we get

$C D+A D+B C+A B>C A+C A$

$\therefore C D+A D+B C+A B>2 C A$