Question:
In the given figure, RQ is a tangent to the circle with centre O. If SQ = 6 cm and QR = 4 cm, then OR =
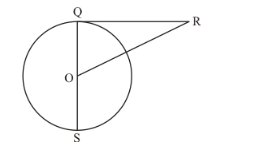
(a) 8 cm
(b) 3 cm
(c) 2.5 cm
(d) 5 cm
Solution:
It is given that,
SQ = 6 cm
Since SQ passes through the centre of the circle O, it is the diameter. Therefore, the radius,
OQ = 3 cm
Also, given is
QR = 4
We know that the radius will always be perpendicular to the tangent at the point of contact. Therefore, OQ is perpendicular to OR. We can find the length of OR by using Pythagoras theorem. We have,
$O R^{2}=O Q^{2}+Q R^{2}$
$O R^{2}=3^{2}+4^{2}$
$O R^{2}=9+16$
$O R^{2}=25$
$O R=5$
Therefore option (d) is the correct answer.
