Question:
In the given figure, the sides CB and BA of ∆ABC have been produced to D and E, respectively, such that ∠ABD = 110° and ∠CAE = 135°. Then ∠ACB = ?
(a) 65°
(b) 45°
(c) 55°
(d) 35°
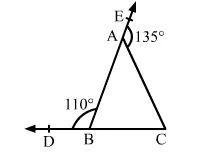
Solution:
(a) 65°
We have :
$\angle A B D+\angle A B C=180^{\circ} \quad[\because C B D$ is a straight line $]$
$\Rightarrow 100^{\circ}+\angle A B C=180^{\circ}$
$\Rightarrow \angle A B C=70^{\circ}$
Side AB of triangle ABC is produced to E.
$\therefore \angle C A E=\angle A B C+\angle A C B$
$\Rightarrow 135^{\circ}=70^{\circ}+\angle A C B$
$\Rightarrow \angle A C B=65^{\circ}$
