In the given figure, there are two concentric circles with centre O

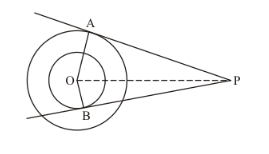
The figure given the question is

From the property of tangents we know that the radius of the circle will always be perpendicular to the tangent at the point of contact. Therefore, OA is perpendicular to AP and triangle OAP is a right triangle. Therefore,

$O P^{2}=A P^{2}+O A^{2}$

$=12^{2}+5^{2}$

$=144+25$

$O P=\sqrt{169}$

$=13$

Now consider the smaller circle. Here again the radius OB will be perpendicular to the tangent BP. Therefore, triangle OBP is a right triangle. Hence we have,

$B P^{2}=O P^{2}-O B^{2}$

$=13^{2}-3^{2}$

$=169-9$

$B P=\sqrt{160}$

$=4 \sqrt{10}$

Thus we have found that the length of BP is $4 \sqrt{10}$.