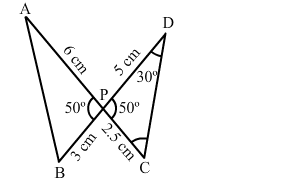
In the given figure, two lines segments AC and BD intersect each other at the point P such that PA = 6 cm,

(d) 100°

In $\triangle A P B$ and $\triangle D P C$, we have :

$\angle A P B=\angle D P C=50^{\circ}$

$\frac{A P}{B P}=\frac{6}{3}=2$

$\frac{D P}{C P}=\frac{5}{2.5}=2$

Hence, $\frac{A P}{B P}=\frac{D P}{C P}$

Applying $S A S$ theorem, we conclude that $\triangle A P B \sim \triangle D P C$.

$\therefore \angle P B A=\angle P C D$

In $\triangle D P C$, we have:

$\angle C D P+\angle C P D+\angle P C D=180^{\circ}$

$\Rightarrow \angle P C D=180^{\circ}-\angle C D P-\angle C P D$

$\Rightarrow \angle P C D=180^{\circ}-30^{\circ}-50^{\circ}$

$\Rightarrow \angle P C D=100^{\circ}$

Therefore, $\angle P B A=100^{\circ}$