In the given figure, $X Y \| A C$ and $X Y$ divides $\triangle A B C$ into two regions, equal in area. Show that $\frac{A X}{A B}=\frac{(2-\sqrt{2})}{2}$.
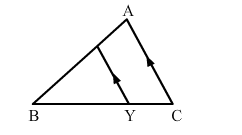
In $\triangle A B C$ and $\triangle B X Y$, we have:
$\angle B=\angle B$
$\angle B X Y=\angle B A C \quad$ (Corresponding angles)
Thus, $\triangle A B C \sim \triangle B X Y \quad($ AA criterion $)$
$\therefore \frac{\operatorname{ar}(\triangle A B C)}{\operatorname{ar}(\triangle B X Y)}=\frac{A B^{2}}{B X^{2}}=\frac{A B^{2}}{(A B-A X)^{2}} \quad \cdots(\mathrm{i})$
Also, $\frac{\operatorname{ar}(\triangle A B C)}{\operatorname{ar}(\triangle B X Y)}=\frac{2}{1}\{\because \operatorname{ar}(\triangle B X Y)=\operatorname{ar}($ trapezium $A X Y C)\} \quad \ldots($ ii $)$
From $(\mathrm{i})$ and $(\mathrm{ii})$, we have :
$\frac{A B^{2}}{(A B-A X)^{2}}=\frac{2}{1}$
$\Rightarrow \frac{A B}{(A B-A X)}=\sqrt{2}$
$\Rightarrow \frac{(A B-A X)}{A B}=\frac{1}{\sqrt{2}}$
$\Rightarrow 1-\frac{A X}{A B}=\frac{1}{\sqrt{2}}$
$\Rightarrow \frac{A X}{A B}=1-\frac{1}{\sqrt{2}}=\frac{\sqrt{2}-1}{\sqrt{2}}=\frac{(2-\sqrt{2})}{2}$
