Interference fringes are observed on a screen by illuminating two thin slits $1 \mathrm{~mm}$ apart with a light source $(\lambda=632.8 \mathrm{~nm})$. The distance between the screen and the slits is $100 \mathrm{~cm}$. If a bright fringe is observed on a screen at a distance of $1.27 \mathrm{~mm}$ from the central bright fringe, then the path difference between the waves, which are reaching this point from the slits is close to :
Correct Option: 1
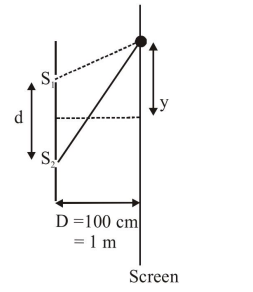
$\mathrm{y}=\frac{\mathrm{n} \mathrm{D} \lambda}{\mathrm{d}}$
$\mathrm{n}=\frac{\mathrm{yd}}{\mathrm{D} \lambda}=\frac{1.27 \times 10^{-3} \times 10^{-3}}{1 \times 632.8 \times 10^{-9}}=2$
Path difference $\Delta x=n \lambda$
$=2 \times 632.8 \mathrm{~nm}$
$=1265.6 \mathrm{~nm}$
$=1.27 \mu \mathrm{m}$
