Question:
Let $A_{1}$ be the area of the region bounded by the curves $y=\sin x, y=\cos x$ and $y$-axis in the first quadrant. Also, let $A_{2}$ be the area of the region bounded by the curves $y=\sin x, y=\cos x, x$-axis and $x=\frac{\pi}{2}$ in the first quadrant. Then,
Correct Option: , 4
Solution:
$A_{1}+A_{2}=\int_{0}^{\pi / 2} \cos x \cdot d x=\left.\sin x\right|_{0} ^{\pi / 2}=1$
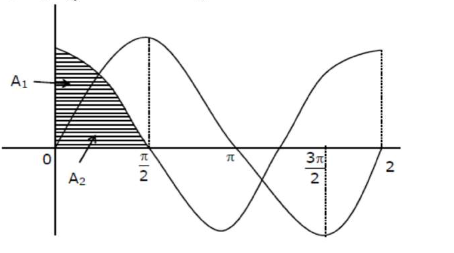
$A_{1}=\int_{0}^{\pi / 4}(\cos x-\sin x) d x=\left.(\sin x+\cos x)\right|_{0} ^{\pi / 4}=\sqrt{2}-1$
$\therefore A_{2}=1-(\sqrt{2}-1)=2-\sqrt{2}$
$\therefore \frac{A_{1}}{A_{2}}=\frac{\sqrt{2}-1}{\sqrt{2}(\sqrt{2}-1)}=\frac{1}{\sqrt{2}}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.