Let A = {2, 3, 5, 7, 11, 13}, B = {5, 7, 9, 11, 15} be subsets of U = {2, 3, 5, 7, 9, 11, 13, 15}.
Using Venn diagrams, verify that:
(i) $\left(A \cup B^{\prime}\right)=\left(A^{\prime} \cap B^{\prime}\right)$
(ii) $(A \cap B)^{\prime}=\left(A^{\prime} \cup B^{\prime}\right)$
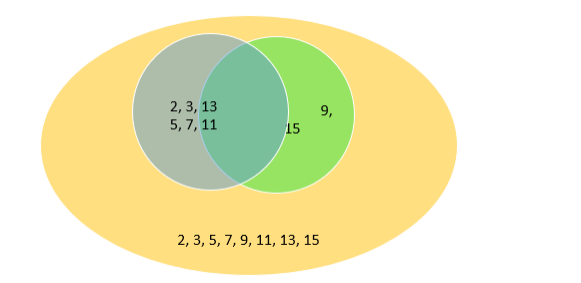
(i) Here blue region denotes set A - B
The green region denotes set B – A
The overlapping region denotes $A \cap B$, and the orange region denotes the universal set U.
From the Venn diagram we get $\left(A^{U} B^{\prime}\right)=\{2,3,5,7,11,13\}$ ( $B$ ' is the set excluding those elements present in set B i.e. A - B region)
$A^{\prime}=\{9,15\}$ and $B^{\prime}=\{2,3,13\}$
Therefore $\mathrm{A}^{\prime} \mathrm{D}_{\mathrm{B}}^{\prime}=\{\}$
Therefore $\left(A \cup B^{\prime}\right)^{\neq}\left(A^{\prime} \cap B^{\prime}\right)[$ Verified $]$
(ii) From the Venn diagram we get $(A \cap B)^{\prime}=\{2,3,9,13,15\}$ (elements except those present in $A \cap B$ )
$\left(A^{\prime} \cup B^{\prime}\right)=\{2,3,9,13,15\}$
Therefore, $(A \cap B)^{\prime}=\left(A^{\prime} \cup B^{\prime}\right)[$ Verified $]$
