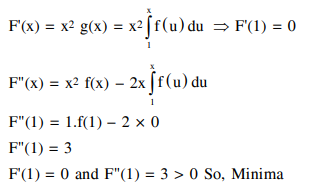Question: Let a function $f:[0,5] \rightarrow \mathbf{R}$ be continuous, $f(1)=3$ and $F$ be defined as :
$F(x)=\int_{1}^{x} t^{2} g(t) d t$, where $g(t)=\int_{1}^{t} f(u) d u$.
Then for the function $F$, the point $x=1$ is:
a point of local minima.
not a critical point.
a point of inflection.
a point of local maxima.
Correct Option: 1
Solution: