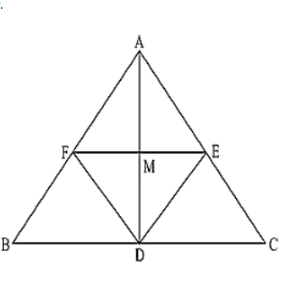
Let ABC be an isosceles triangle in which AB = AC. If D, E, F be the mid points of the, sides BC, CA and AB
Question:
Let ABC be an isosceles triangle in which AB = AC. If D, E, F be the mid points of the, sides BC, CA and AB respectively, show that the segment AD and EF bisect each other at right angles.
Solution:
Since D, E and F are mid-points of sides BC, CA and AB respectively.
∴ AB ∥ DE and AC ∥ DF
∴ AF ∥ DE and AE ∥ DF
ABDE is a parallelogram.
AF = DE and AE = DF
(1/2) AB = DE and (1/2) AC = DF
DE = DF [Since, AB = AC]
AE = AF = DE = DF
ABDF is a rhombus.
⟹ AD and FE bisect each other at right angle.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
