Question:
Let $\mathrm{AD}$ and $\mathrm{BC}$ be two vertical poles at $\mathrm{A}$ and $\mathrm{B}$ respectively on a horizontal ground. If $A D=8 \mathrm{~m}, B C=11 \mathrm{~m}$ and $A B=10$ $\mathrm{m}$; then the distance (in meters) of a point $\mathrm{M}$ on $\mathrm{AB}$ from the point $\mathrm{A}$ such that $\mathrm{MD}^{2}+\mathrm{MC}^{2}$ is minimum is_____________.
Solution:
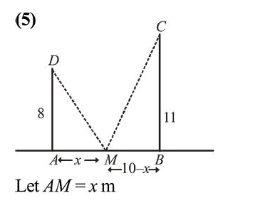
Let $A M=x \mathrm{~m}$
$\therefore(M D)^{2}+(M C)^{2}=64+x^{2}+121+(10-x)^{2}=f(x)$ (say)
$f^{\prime}(x)=2 x-2(10-x)=0$
$\Rightarrow 4 x=20 \Rightarrow x=5$
$f^{\prime \prime}(x)=2-2(-1)>0$
$\therefore f(x)$ is minimum at $x=5 \mathrm{~m}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.