Question:
Let $\boldsymbol{f}: \mathrm{R} \rightarrow \mathrm{R}$ be defined as $\boldsymbol{f}(\mathrm{x})=2 \mathrm{x}-1$ and $\mathrm{g}: \mathrm{R}-\{1\} \rightarrow \mathrm{R}$ be defined as $\mathrm{g}(\mathrm{x})=\frac{\mathrm{x}-\frac{1}{2}}{\mathrm{x}-1}$. Then the composition function $f(g(x))$ is :
Correct Option: , 4
Solution:
$f(g(x))=2 g(x)-1$
$=2 \frac{\left(\frac{x-\frac{1}{2}}{2}\right)}{x-1}=\frac{x}{x-1}$
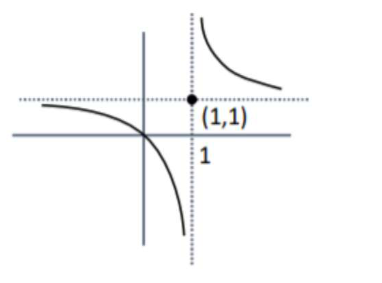
$f(g(x))=1+\frac{1}{x-1}$
one-one, into