Question:
Let $f: \mathrm{R} \rightarrow \mathrm{R}$ be a function defined by $f(x)=\max \left\{x, x^{2}\right\}$. Let $\mathrm{S}$ denote the set of all points in $\mathrm{R}$, where $f$ is not differentiable. Then:
Correct Option: 1
Solution:
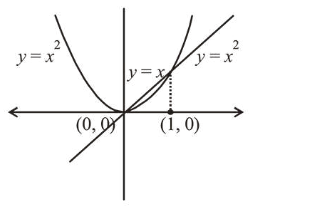
$f(x)=\max \cdot\left\{x, x^{2}\right\}$
$\Rightarrow f(x)=\left\{\begin{array}{cc}x^{2}, & x<0 \\ x, & 0 \leq x<1 \\ x^{2}, & x \geq 1\end{array}\right.$
$\therefore f(x)$ is not differentiable at $x=0,1$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.