Question:
Let $f:(-1,1) \rightarrow \mathbf{R}$ be a function defined by $f(x)=\max$ $\left\{-|x|,-\sqrt{1-x^{2}}\right\} .$ If $\mathrm{K}$ be the set of all points at which $f$ is not differentiable, then $\mathrm{K}$ has exactly:
Correct Option: , 3
Solution:
Consider the function
$f(x)=\max \left\{-|x|,-\sqrt{1-x^{2}}\right\}$
Now, the graph of the function
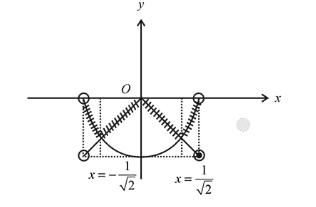
From the graph, it is clear that $f(x)$ is not differentiable at $x=0,-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}$
Then, $K=\left\{-\frac{1}{\sqrt{2}}, 0, \frac{1}{\sqrt{2}}\right\}$
Hence, $K$ has exactly three elements.
