Question:
Let $f(x)=\left\{\begin{array}{cc}\max \left\{|x|, x^{2}\right\} & |x| \leq 2 \\ 8-2|x|, & 2<|x| \leq 4\end{array}\right.$
Let $\mathrm{S}$ be the set of points in the interval $(-4,4)$ at which $f$ is not differentiable. Then $\mathrm{S}$ :
Correct Option: , 2
Solution:
Given $f(x)=\left\{\begin{array}{cc}\max \left\{|x|, x^{2}\right\} & |x| \leq 2 \\ 8-2|x| & 2<|\mathrm{x}| \leq 4\end{array}\right.$
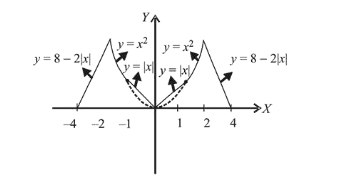
$\because f(x)$ is not differentiable at $-2,-1,0,1$ and 2 .
$\therefore S=\{-2,-1,0,1,2\}$
