Question:
Let $f(x)=5-|x-2|$ and $g(x)=|x+1|, x \in$ R. If $f(x)$ attains maximum value at $\alpha$ and $g(x)$ attains minimum value at $\beta$,
then $\lim _{x \rightarrow-\alpha \beta} \frac{(x-1)\left(x^{2}-5 x+6\right)}{x^{2}-6 x+8}$ is equal to :
Correct Option: 1,
Solution:
$f(x)=5-|x-2|$
Graph of $y=f(x)$
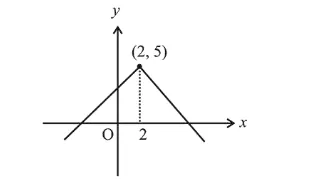
By the graph $f(x)$ is maximum at $x=2 \therefore \alpha=2$
$g(x)=|x+1|$
Graph of $y=g(x)$
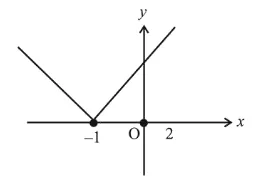
By the graph $g(x)$ is minimum at $x=-1$
$\therefore \quad \beta=-1$
Now, $\lim _{x \rightarrow 2} \frac{(x-1)(x-2)(x-3)}{(x-2)(x-4)}$
$=\lim _{x \rightarrow 2} \frac{(x-1)(x-3)}{x-4}=\frac{1}{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.