Let $\mathrm{P}$ be a variable point on the parabola $y=4 x^{2}+1 .$ Then, the locus of the mid-point of the point $P$ and the foot of the perpendicular drawn from the point $\mathrm{P}$ to the line $\mathrm{y}=\mathrm{x}$ is :
Correct Option: , 2
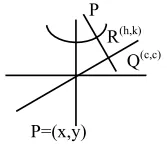
$\frac{\mathrm{K}-\mathrm{C}}{\mathrm{h}-\mathrm{C}}=-1$
$\mathrm{C}=\frac{\mathrm{h}+\mathrm{K}}{2} \quad \mathrm{P}(\mathrm{x}, \mathrm{y})$
$R=\left(\frac{x+C}{2}, \frac{y+C}{2}\right)$
$R=\left(\frac{x}{2}+\frac{h}{4}+\frac{K}{4}, \frac{y}{2}+\frac{h}{4}+\frac{k}{4}\right)$
$h=\frac{x}{2}+\frac{h}{4}+\frac{K}{4}$
$\mathrm{K}=\frac{\mathrm{y}}{2}+\frac{\mathrm{h}}{4}+\frac{\mathrm{K}}{4}$
$\Rightarrow x=\frac{3 h}{2}-\frac{K}{2}, y=\frac{3 K}{2}-\frac{h}{2}$
$\mathrm{Y}=4 \mathrm{x}^{2}+1$
$\left(\frac{3 \mathrm{k}-\mathrm{h}}{2}\right)=4\left(\frac{3 \mathrm{~h}-\mathrm{k}}{2}\right)^{2}+1$
