Let $\mathrm{P}$ be the point of intersection of the common tangents to the parabola $y^{2}=12 x$ and hyperbola $8 x^{2}-y^{2}=8$. If $\mathrm{S}$ and $\mathrm{S}^{\prime}$ denote the foci of the hyperbola where $S$ lies on the positive $x$-axis then P divides SS ' in a ratio :
Correct Option: , 3
Equation of tangent to $y^{2}=12 x$ is $y=m x+\frac{3}{m}$ Equation of tangent to
$\frac{x^{2}}{1}-\frac{y^{2}}{8}=1$ is $y=m x \pm \sqrt{m^{2}-8}$
$\because$ parabola and hyperbola have common tangent.
$\therefore \quad \frac{3}{m}=\pm \sqrt{m^{2}-8} \Rightarrow \frac{9}{m^{2}}=m^{2}-8$
Put $m^{2}=u$
$u^{2}-8 u-9=0 \Rightarrow u^{2}-9 u+u-9=0$
$\Rightarrow(u+1)(u-9)=0$
$\because u=m^{2} \geq 0 \Rightarrow u=m^{2}=9 \Rightarrow m=\pm 3$
$\therefore$ equation of tangent is $y=3 x+1$
or $y=-3 x-1$
$\therefore$ intersection point is $P\left(-\frac{1}{3}, 0\right)$.
$e=\sqrt{1+\frac{b^{2}}{a^{2}}} \Rightarrow e=\sqrt{1+\frac{8}{1}} \Rightarrow e=3$
$\therefore$ foci $(\pm 3,0)$
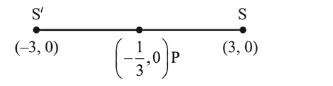
$\frac{S P}{S P^{\prime}}=\frac{3+\frac{1}{3}}{3-\frac{1}{3}}=\frac{10}{8}=\frac{5}{4}$
