Question:
Let $P(h, k)$ be a point on the curve $y=x^{2}+7 x+2$, nearest to the line, $y=3 x-3$. Then the equation of the normal to the curve at $P$ is :
Correct Option: 1
Solution:
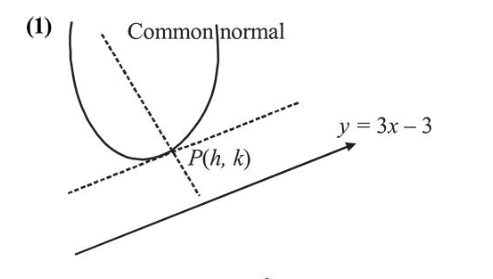
The given curve is, $y=x^{2}+7 x+2$
$\Rightarrow \frac{d y}{d x}=2 x+7$
$\left(\frac{d y}{d x}\right)_{(h, k)}=2 h+7$
The tangent at $P(h, k)$ will be parallel to given line
$2 h+7=3 \Rightarrow h=-2$
Point $P(h, k)$ lies on curve
$k=(-2)^{2}-7 \times 2+2=-8$
Slope of normal at point $P(-2,-8)=-\frac{1}{3}$
$\therefore$ The equation of normal to the cuve at $P$ is
$x+3 y+26=0$
