Let $S$ and $S^{\prime}$ be the foci of an ellipse and $B$ be any one of the extremities of its minor axis. If $\Delta \mathrm{S}^{\prime} \mathrm{BS}$ is a right angled triangle with right angle at $\mathrm{B}$ and area $\left(\Delta \mathrm{S}^{\prime} \mathrm{BS}\right)=8 \mathrm{sq}$. units, hen the length of a latus rectum of the ellipse is :
Correct Option: 1
$\because \triangle S B S$ is right angled triangle, then
$($ Slope of $B S) \times\left(\right.$ Slope of $\left.B S^{\prime}\right)=-1$
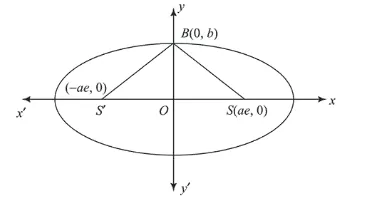
$\frac{b}{-a e} \times \frac{b}{a e}=-1$
$b^{2}=a^{2} e^{2}$ .....(1)
Since, area of $\triangle S^{\prime} B S=8$
$\Rightarrow \quad \frac{1}{2} \cdot 2 a e \cdot b=8$
$b^{2}=8$ ....(2)
From eq $^{n}$ (1)
$a^{2} e^{2}=8$
Also,
$e^{2}=1-\frac{b^{2}}{a^{2}}$
$\Rightarrow a^{2} e^{2}=a^{2}-b^{2}$
$\Rightarrow 8=a^{2}-8$
$\Rightarrow a^{2}=16$
Hence, required length of latus rectum $=\frac{2 b^{2}}{a}=\frac{2(8)}{4}$
$=4$ units
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.