Let $S_{1}: x^{2}+y^{2}=9$ and $S_{2}:(x-2)^{2}+y^{2}=1$ Then the locus of center of a variable circle $S$ which touches $S_{1}$ internally and $S_{2}$ externally always passes through the points:
Correct Option: 3,
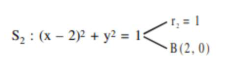
$\because \mathrm{c}_{1} \mathrm{c}_{2}=\mathrm{r}_{1}-\mathrm{r}_{2}$
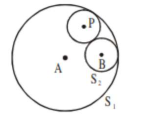
$\therefore$ given circle are touching internally
Let a veriable circle with centre $\mathrm{P}$ and radius
r
$\Rightarrow \mathrm{PA}=r_{1}-r$ and $\mathrm{PB}=\mathrm{r}_{2}+\mathrm{r}$
$\Rightarrow \mathrm{PA}+\mathrm{PB}=\mathrm{r}_{1}+\mathrm{r}_{2}$
$\Rightarrow \mathrm{PA}+\mathrm{PB}=4(>\mathrm{AB})$
$\Rightarrow$ Locus of $P$ is an ellipse with foci at $A(0,0)$ and $B(2,0)$ and length of major axis is $2 \mathrm{a}=4$,
$e=\frac{1}{2}$
$\Rightarrow$ centre is at $(1,0)$ and $b^{2}=a^{2}\left(1-e^{2}\right)=3$
if $x$-ellipse
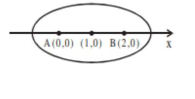
which is satisfied by $\left(2, \pm \frac{3}{2}\right)$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.