Question:
Let the centroid of an equilateral triangle $\mathrm{ABC}$ be at the origin. Let one of the sides of the equilateral triangle be along the straight line $x+y=3 .$ If $R$ and $r$ be the radius of circumcircle and incircle respectively of $\triangle \mathrm{ABC}$, then $(\mathrm{R}+\mathrm{r})$ is equal to :
Correct Option: 1
Solution:
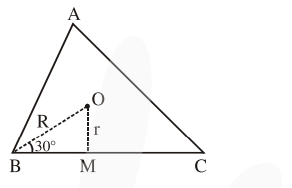
$\mathrm{r}=\mathrm{OM}=\frac{3}{\sqrt{2}}$
$\& \sin 30^{\circ}=\frac{1}{2}=\frac{\mathrm{r}}{\mathrm{R}} \Rightarrow \mathrm{R}=\frac{6}{\sqrt{2}}$
$\therefore r+R=\frac{9}{\sqrt{2}}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.