Question:
Let the line $\mathrm{L}$ be the projection of the line
$\frac{x-1}{2}=\frac{y-3}{1}=\frac{z-4}{2}$
in the plane $x-2 y-z=3$. If $d$ is the distance of the point $(0,0,6)$ from $\mathrm{L}$, then $\mathrm{d}^{2}$ is equal to__________
Solution:
$L_{1}: \frac{x-1}{2}=\frac{y-3}{1}=\frac{z-4}{2}$
for foot of $\perp \mathrm{r}$ of $(1,3,4)$ on $\mathrm{x}-2 \mathrm{y}-\mathrm{z}-3=0$
$(1+t)-2(3-2 t)-(4-t)-3=0$
$\Rightarrow \mathrm{t}=2$
So foot of $\perp r \triangleq(3,-1,2)$
& point of intersection of $L_{1}$ with plane
is $(-11,-3,-8)$
dr's of $L$ is $<14,2,10>$
$\cong\langle 7,1,5\rangle$
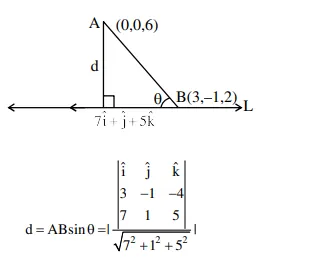
$\Rightarrow d^{2}=\frac{1^{2}+(43)^{2}+(10)^{2}}{49+1+25}=26$
