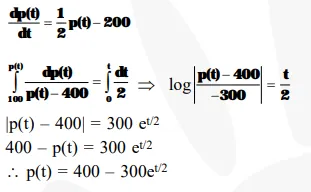Question:
Let the population of rabbits surviving at a time t be governed by the differential equation $\frac{\mathrm{dp}(\mathrm{t})}{\mathrm{dt}}=\frac{1}{2} \mathrm{p}(\mathrm{t})-200$. If $\mathrm{p}(0)=100$, then $\mathrm{p}(\mathrm{t})$ equals :
Correct Option: 1
Solution: