Let the tangent to the circle $x^{2}+y^{2}=25$ at the point $\mathrm{R}(3,4)$ meet $\mathrm{x}$-axis and $\mathrm{y}$-axis at point $\mathrm{P}$ and $\mathrm{Q}$, respectively. If $\mathrm{r}$ is the radius of the circle passing through the origin $\mathrm{O}$ and having centre at the incentre of the triangle $\mathrm{OPQ}$, then $\mathrm{r}^{2}$ is equal to
Correct Option: , 3
Tangent to circle $3 x+4 y=25$
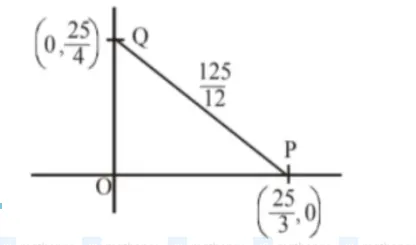
$\mathrm{OP}+\mathrm{OQ}+\mathrm{OR}=25$
Incentre $=\left(\frac{\frac{25}{4} \times \frac{25}{3}}{25}, \frac{\frac{25}{4} \times \frac{25}{3}}{25}\right)$
$=\left(\frac{25}{12}, \frac{25}{12}\right)$
$\therefore \mathrm{r}^{2}=2\left(\frac{25}{12}\right)^{2}=2 \times \frac{625}{144}=\frac{625}{72}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.