Let y=y(x) be the solution of the differential equation

Sol. $\cos x(3 \sin x+\cos x+3) \mathrm{dy}$

$=(1+y \sin x(3 \sin x+\cos x+3)) \mathrm{d} x$

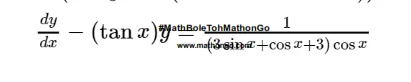
I.F. $=e^{\int-\tan x d x}=e^{(n \cos x \mid}=|\cos x|$

$=\cos x \forall x \in\left[0, \frac{\pi}{2}\right)$

Solution of D. E

$y(\cos x)=\int(\cos x) \cdot \frac{1}{\cos x(3 \sin x+\cos x+3)} d x+C$

$y(\cos x)=\int \frac{d x}{3 \sin x+\cos x+3} d x+C$

$y(\cos x)=\int \frac{\left(\sec ^{2} \frac{x}{2}\right)}{2 \tan ^{2} \frac{x}{2}+6 \tan \frac{x}{2}+4} d x+C$

Now $I_{1}=\int \frac{\left(\sec ^{2} \frac{x}{2}\right)}{2\left(\tan ^{2} \frac{x}{2}+3 \tan \frac{x}{2}+2\right)} d x+C$

Put $\tan \frac{\mathrm{x}}{2}=\mathrm{t} \Rightarrow \frac{1}{2} \sec ^{2} \frac{\mathrm{x}}{2} \mathrm{~d} \mathrm{x}=\mathrm{dt}$

$\mathrm{I}_{1}=\int \frac{\mathrm{dt}}{\mathrm{t}^{3}+3 \mathrm{t}+2}=\int \frac{\mathrm{dt}}{(\mathrm{t}+2)(\mathrm{t}+1)}$

$=\int\left(\frac{1}{t+1}-\frac{1}{t+2}\right) \mathrm{dt}$

$=\ell \mathrm{n}\left|\left(\frac{\mathrm{t}+1}{\mathrm{t}+2}\right)\right|=\ell \mathrm{n}\left|\left(\frac{\tan \frac{\mathrm{x}}{2}+1}{\tan \frac{\mathrm{x}}{2}+2}\right)\right|$

So solution of D. E

$y(\cos x)=\ln \left|\frac{1+\tan \frac{x}{2}}{2+\tan \frac{x}{2}}\right|+C$

$\Rightarrow y(\cos x)=\ell n\left(\frac{1+\tan \frac{x}{2}}{2+\tan \frac{x}{2}}\right)+C \quad$ for $0 \leq x<\frac{\pi}{2}$

Now, it is given $y(0)=0$

$\Rightarrow 0=\ell \mathrm{n}\left(\frac{1}{2}\right)+\mathrm{C} \Rightarrow \mathrm{C}=\ell \mathrm{n} 2$

$\Rightarrow y(\cos x)=\ell n\left(\frac{1+\tan \frac{x}{2}}{2+\tan \frac{x}{2}}\right)+C \quad$ for $0 \leq x<\frac{\pi}{2}$

Now, it is given $y(0)=0$

For $x=\frac{\pi}{3}$

$y\left(\frac{1}{2}\right)=\ln \left(\frac{1+\frac{1}{\sqrt{3}}}{2+\frac{1}{\sqrt{3}}}\right)+\ell \mathrm{n} 2$

$\mathrm{y}=2 \ell \mathrm{n}\left(\frac{2 \sqrt{3}+10}{11}\right)$