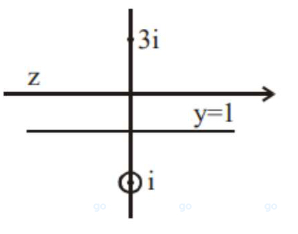
Let $z$ and $w$ be two complex numbers such that
$\mathrm{w}=\mathrm{z} \overline{\mathrm{z}}-2 \mathrm{z}+2,\left|\frac{\mathrm{z}+\mathrm{i}}{\mathrm{z}-3 \mathrm{i}}\right|=1 \quad$ and $\quad \operatorname{Re}(\mathrm{w})$ has
minimum value. Then,the minimum value of
$\mathrm{n} \in \mathbb{N}$ for which $\mathrm{w}^{\mathrm{n}}$ is real, is equal to_____________.
$\omega=z \bar{z}-2 z+2$
$\left|\frac{z+i}{z-3 i}\right|=1$
$\Rightarrow \quad|z+i|=|z-3 i|$
$\Rightarrow \quad z=x+i, \quad x \in \mathbb{R}$
$\omega=(x+i)(x-i)-2(x+i)+2$
$=x^{2}+1-2 x-2 i+2$
$\operatorname{Re}(\omega)=x^{2}-2 x+3$
For $\min (\operatorname{Re}(\omega)), x=1$
$\Rightarrow \quad \omega=2-2 i=2(1-i)=2 \sqrt{2} e^{-i \frac{\pi}{4}}$
$\omega^{n}=(2 \sqrt{2})^{n} e^{-i \frac{n \pi}{4}}$
For real $\backslash \&$ minimum value of $\mathrm{n} \mathrm{n}=4$