Magnetic fields at two points on the axis of a circular coil at a distance

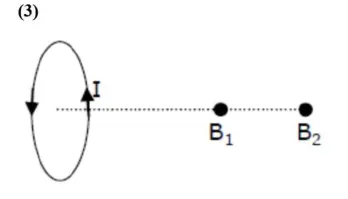
$B=\frac{\mu_{0} N i R^{2}}{2\left(R^{2}+x^{2}\right)^{3 / 2}}$

at $\mathrm{x}_{1}=0.05 \mathrm{~m}, \mathrm{~B}_{1}=\frac{\mu_{0} \mathrm{NiR}^{2}}{2\left(\mathrm{R}^{2}+(0.05)^{2}\right)^{3 / 2}}$

at $\mathrm{x}_{2}=0.2 \mathrm{~m}, \mathrm{~B}_{2}=\frac{\mu_{0} \mathrm{NiR}^{2}}{2\left(\mathrm{R}^{2}+(0.2)^{2}\right)^{3 / 2}}$

$\frac{B_{1}}{B_{2}}=\frac{\left(R^{2}+0.04\right)^{3 / 2}}{\left(R^{2}+0.0025\right)^{3 / 2}}$

$\left(\frac{8}{1}\right)^{2 / 3}=\frac{R^{2}+0.04}{R^{2}+0.0025}$

$4\left(R^{2}+0.0025\right)=R^{2}+0.04$\

$3 R^{2}=0.04-0.0100$

$\mathrm{R}^{2}=\frac{0.03}{3}=0.01$

$\mathrm{R}=\sqrt{0.01}=0.1 \mathrm{~m}$