Magnitude of magnetic field (in SI units)

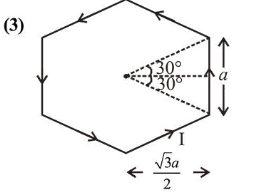
Magnetic field due to one side of hexagon

$B=\frac{\mu_{0} I}{4 \pi \frac{\sqrt{3} a}{2}}\left(\sin 30^{\circ}+\sin 30^{\circ}\right)$

$\Rightarrow B=\frac{\mu_{0} I}{2 \sqrt{3} a}\left(\frac{1}{2}+\frac{1}{2}\right)=\frac{\mu_{0} I}{2 \sqrt{3} a \pi}$

Now, magnetic field due to one hexagon coil

$B=6 \times \frac{\mu_{0} I}{2 \sqrt{3} a \pi}$

Again magnetic field at the centre of hexagonal shape coil of 50 turns,

$B=50 \times 6 \times \frac{\mu_{0} I}{2 \sqrt{3} a \pi}$             $\left[\because a=\frac{10}{100}=0.1 \mathrm{~m}\right]$

or, $B=\frac{150 \mu_{0} I}{\sqrt{3} \times 0.1 \times \pi}=500 \sqrt{3} \frac{\mu_{0} I}{\pi}$