Mark the tick against the correct answer in the following:

To Find: The range of $\operatorname{cosec}^{-1}(x)$

Here,the inverse function is given by $y=\mathrm{f}^{-1}(x)$

The graph of the function $y=\operatorname{cosec}^{-1}(x)$ can be obtained from the graph of

$Y=\operatorname{cosec} x$ by interchanging $x$ and $y$ axes.i.e, if $(a, b)$ is a point on $Y=\operatorname{cosec} x$ then $(b, a)$ is the point on the function $y=\operatorname{cosec}^{-1}(x)$

Below is the Graph of the range of $\operatorname{cosec}^{-1}(x)$

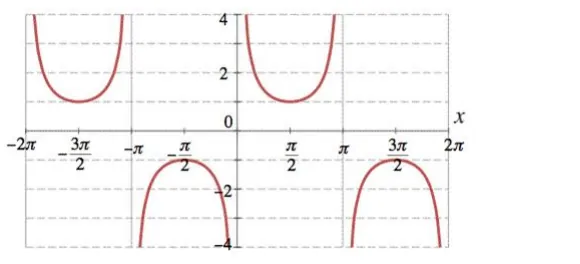
From the graph it is clear that the range of $\operatorname{cosec}^{-1}(x)$ is restricted to interval

$\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]-\{0\}$