Match the following columns:

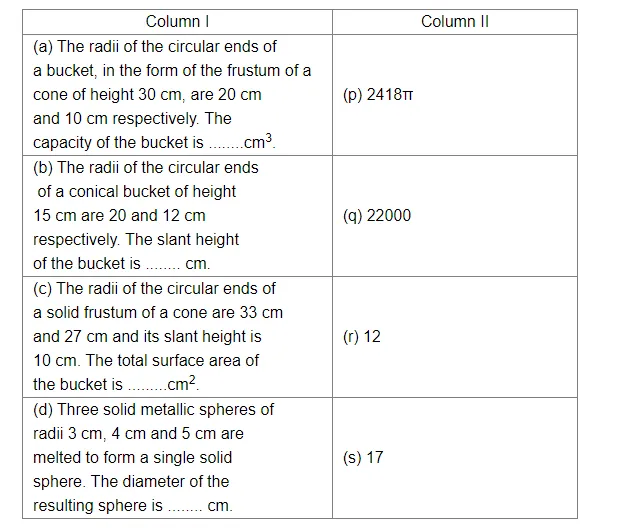
(a)

Volume of the sphere $=\frac{4}{3} \pi r^{3}$

$=\left(\frac{4}{3} \pi \times(8)^{3}\right) \mathrm{cm}^{3}$

Volume of each cone $=\frac{1}{3} \pi r^{2} h$

$=\frac{1}{3} \pi \times(8)^{2} \times 4 \mathrm{~cm}^{3}$

Number of cones formed $=\frac{\text { Volume of the sphere }}{\text { Volume of each cone }}$

$=\frac{4 \pi \times 8 \times 8 \times 8 \times 3}{3 \times \pi \times 8 \times 8 \times 4}$

$=8$

Hence, $(a) \Rightarrow(q)$

(b)

Volume of the earth dug out $=$ Volume of the cylinder

$=\pi r^{2} h$

$=\frac{22}{7} \times 7 \times 7 \times 20$

Let the height of the platform be $h$.

Then, volume of the platform = volume of the cuboid

$=(44 \times 14 \times h) \mathrm{m}^{3}$

Therefore,

$\frac{22}{7} \times 7 \times 7 \times 20=44 \times 14 \times h$

$\Rightarrow 3080=616 \times h$

$\Rightarrow h=\frac{3080}{616}$

$\Rightarrow h=5 \mathrm{~m}$

Hence, $(b) \Rightarrow(s)$

(c)

Volume of the sphere

$=\frac{4}{3} \pi r^{3}$

$=\frac{4}{3} \pi \times 6 \times 6 \times 6$

Let $\mathrm{h}$ be the height of the cylinder.

Then, volume of the cylinder $=\pi r^{2} h$

$=\pi \times 4 \times 4 \times \mathrm{h}$

Therefore,

$\frac{4}{3} \pi \times 6 \times 6 \times 6=\pi \times 4 \times 4 \times \mathrm{h}$

$\Rightarrow \frac{4}{3} \times 6 \times 6 \times 6=4 \times 4 \times \mathrm{h}$

$\Rightarrow 228=16 \times \mathrm{h}$

$\Rightarrow \mathrm{h}=\frac{228}{16}$

$\Rightarrow \mathrm{h}=18 \mathrm{~cm}$

Hence, $(c) \Rightarrow(p)$

(d)

Let the radii of the spheres be $R$ and $r$ respectively.

Then, ratio of their volumes $=\frac{\frac{4}{3} \pi R^{3}}{\frac{4}{3} \pi r^{3}}$

Therefore,

$\frac{\frac{4}{3} \pi R^{3}}{\frac{4}{3} \pi r^{3}}=\frac{64}{27}$

$\Rightarrow \frac{R^{3}}{r^{3}}=\frac{64}{27}$

$\Rightarrow\left(\frac{R}{r}\right)^{3}=\left(\frac{4}{3}\right)^{3}$

$\Rightarrow \frac{R}{r}=\frac{4}{3}$

Hence, the ratio of their surface areas $=\frac{4 \pi R^{2}}{4 \pi r^{2}}$

$=\frac{R^{2}}{r^{2}}$

$=\left(\frac{R}{r}\right)^{2}$

$=\left(\frac{4}{3}\right)^{2}$

$=\frac{16}{9}$

$=16: 9$

Hence, $(d) \Rightarrow(r)$