Model a torch battery of length $l$ to be made up of a thin cylindrical bar of radius ' $a$ ' and a concentric thin cylindrical shell of radius ' $b$ ' filled in between with an electrolyte of resistivity $\rho$ (see figure). If the battery is connected to a resistance of value $R$, the maximum Joule heating in $R$ will take place for:
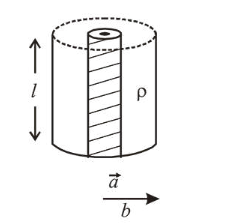
Correct Option: , 2
(2) Maximum power in external resistance is generated when it is equal to internal resistance of battery i.e., $P_{R}$ maximum when $r=R$
The maximum Joule heating in $R$ will take place for, the resistance of small element
$\Delta R=\frac{\rho d r}{2 \pi r l} \Rightarrow R=\frac{\rho}{2 \pi l} \int_{a}^{b} \frac{d r}{r}$
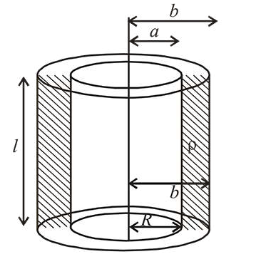
or, $R=\frac{\rho}{2 \pi l} \ln \frac{b}{a}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.