Moment of inertia of a cylinder of mass $M$, length $L$ and radius $R$ about an axis passing through its centre and perpendicular to the axis of the cylinder is
$I=M\left(\frac{R^{2}}{4}+\frac{L^{2}}{12}\right) .$ If such a cylinder is to be made for a
given mass of a material, the ratio $L / R$ for it to have minimum possible $I$ is :
Correct Option: , 3
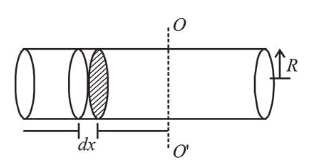
(3) Let there be a cylinder of mass $m$ length $L$ and radius $R$. Now, take elementary disc of radius $R$ and thickness $d x$ at a distance of $x$ from axis $O O^{\prime}$ then moment of inertia about $O O^{\prime}$ of this element.
$d I=\frac{d m R^{2}}{4}+d m x^{2}$
$\Rightarrow I=\int d I=\int \frac{d m R^{2}}{4}+\int_{n=L / 2}^{n=-L / 2} \frac{M}{L} d x \times x^{2}$
Given: $I=\frac{M R^{2}}{4}+\frac{M L^{2}}{12}$
$\Rightarrow I=\frac{M}{4} \times \frac{V}{\pi L}+\frac{M L^{2}}{12} \Rightarrow I=\frac{M V}{4 \pi L}+\frac{M L^{2}}{12}$
$\frac{d I}{d L}=-\frac{m V}{4 \pi L^{2}}+\frac{M \times 2 L}{12}=0$
$\Rightarrow V=\frac{2}{3} \pi L^{3} \Rightarrow \pi R^{2} L=\frac{2}{3} \pi L^{3}$
$\therefore \frac{L}{R}=\sqrt{\frac{3}{2}}$
