Consider a uniform cubical box of side a on a rough floor that is to be moved by applying minimum possible force
Question:
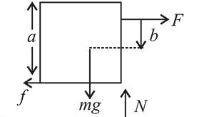
Consider a uniform cubical box of side a on a rough floor that is to be moved by applying minimum possible force $F$ at $a$ point $b$ above its centre of mass (see figure). If the coefficient of friction is $\mu=0.4$, the maximum possible value of $100 x$
$\frac{b}{a}$ for box not to topple before moving is_______
Solution:
(50) For the box to be slide
$F=\mu m g=0.4 \mathrm{mg}$
For no toppling
$F\left(\frac{a}{2}+b\right) \leq m g \frac{a}{2}$
$\Rightarrow 0.4 m g\left(\frac{a}{2}+b\right) \leq m g \frac{a}{2}$
$\Rightarrow 0.2 a+0.4 b \leq 0.5 a$
$\Rightarrow \frac{b}{a} \leq \frac{3}{4}$
i.e. $b \leq 0.75 a$ but this is not possible.
As the maximum value of $b$ can be equal to $0.5 a$.
$\Rightarrow \frac{100 b}{a}=50$
