Question:
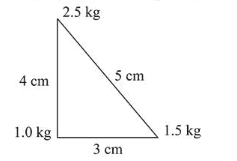
Three point particles of masses $1.0 \mathrm{~kg}, 1.5 \mathrm{~kg}$ and $2.5 \mathrm{~kg}$ are placed at three corners of a right angle triangle of sides $4.0 \mathrm{~cm}, 3.0 \mathrm{~cm}$ and $5.0 \mathrm{~cm}$ as shown in the figure. The center of mass of the system is at a point:
Correct Option: 4,
Solution:
(4)
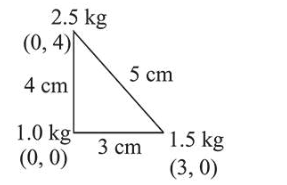
$X_{\mathrm{cm}}=\frac{m_{1} x_{1}+m_{2} x_{2}+m_{3} x_{3}}{m_{1}+m_{2}+m_{3}}$
$X_{c m}=\frac{1 \times 0+1.5 \times 3+2.5 \times 0}{1+1.5+2.5}=\frac{1.5 \times 3}{5}=0.9 \mathrm{~cm}$
$Y_{\mathrm{cm}}=\frac{m_{1} y_{1}+m_{2} y_{2}+m_{3} y_{3}}{m_{1}+m_{2}+m_{3}}$
$Y_{c m}=\frac{1 \times 0+1.5 \times 0+2.5 \times 4}{1+1.5+2.5}=\frac{2.5 \times 4}{5}=2 \mathrm{~cm}$
Hence, centre of mass of system is at point $(0.9,2)$
