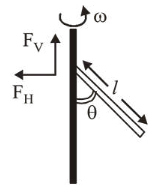
A uniform rod of length ' $l$ ' is pivoted at one of its ends on a vertical shaft of negligible radius. When the shaft rotates at angular speed $\omega$ the rod makes an angle $\theta$ with it (see figure). To find $\theta$ equate the rate of change of angular momentum (direction going into the paper)
$\frac{m l^{2}}{12} \omega^{2} \sin \theta \cos \theta$ about the centre of mass (CM) to the\
torque provided by the horizontal and vertical forces $F_{H}$ and $F_{V}$ about the CM. The value of $\theta$ is then such that:
Correct Option: 4,
(4) Vertical force $=m g$
Horizontal force $=$ Centripetal force $=m \omega^{2} \frac{l}{2} \sin \theta$
Torque due to vertical force $=m g \frac{l}{2} \sin \theta$
Torque due to horizontal force $=m \omega^{2} \frac{l}{2} \sin \theta \frac{l}{2} \cos \theta$
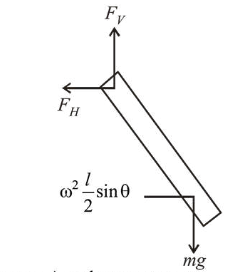
Net Torque $=$ Angular momentum
$m g \frac{l}{2} \sin \theta-m \omega^{2} \frac{l}{2} \sin \theta \frac{l}{2} \cos \theta=\frac{m l^{2}}{12} \omega^{2} \sin \theta \cos \theta$
$\Rightarrow \cos \theta=\frac{3}{2} \frac{g}{\omega^{2} l}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.