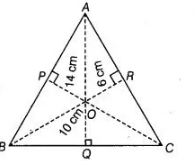
From a point in the interior of an equilateral triangle,

Solution:

Let sides of an equilateral triangle be a $\mathrm{m}$.

Area of $\triangle O A B=\frac{1}{2} \times A B \times O P \quad\left[\because\right.$ area of a triangle $=\frac{1}{2}$ (base $\times$ height) $]$

$=\frac{1}{2} \times a \times 14=7 a \mathrm{~cm}^{2}$ $\ldots(i)$

Area of $\Delta O B C=\frac{1}{2} \times B C \times O Q$

$=\frac{1}{2} \times a \times 10=5 a \mathrm{~cm}^{2}$ $\ldots$ (ii)

Area of $\Delta O A C=\frac{1}{2} \times A C \times O R$

$=\frac{1}{2} \times a \times 6=3 a \mathrm{~cm}^{2}$  .....(iii)

$\therefore$ Area of an equilateral $\triangle A B C=$ Area of $(\triangle O A B+\triangle O B C+\triangle O A C)$

$=(7 a+5 a+3 a)=15 a \mathrm{~cm}^{2}$ ...(iv)

We have, semi-perimeter $s=\frac{a+a+a}{2} \Rightarrow s=\frac{3 a}{2} \mathrm{~cm}$

$\therefore$ Area of an equilateral $\triangle A B C=\sqrt{s(s-a)(s-b)(s-c)}$ [by Heron's formula]

$=\sqrt{\frac{3 a}{2}\left(\frac{3 a}{2}-a\right)\left(\frac{3 a}{2}-a\right)\left(\frac{3 a}{2}-a\right)}$

$=\sqrt{\frac{3 a}{2} \times \frac{a}{2} \times \frac{a}{2} \times \frac{a}{2}}=\frac{\sqrt{3}}{4} a^{2}$ $\ldots(v)$

From Eqs. (iv) and (v).

$\frac{\sqrt{3}}{4} a^{2}=15 a$

$\Rightarrow$ $a=\frac{15 \times 4}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{60 \sqrt{3}}{3}=20 \sqrt{3} \mathrm{~cm}$

On putting $a=20 \sqrt{3}$ in Eq. (v), we get

Area of $\triangle A B C=\frac{\sqrt{3}}{4}(20 \sqrt{3})^{2}$

$=\frac{\sqrt{3}}{4} \times 400 \times 3$

$=300 \sqrt{3} \mathrm{~cm}^{2}$

Hence, the area of an equilateral triangle is $300 \sqrt{3} \mathrm{~cm}^{2}$.