O is the centre of a circle of a radius 8 cm.

First let us draw whatever is given in the question. This will help us understand the problem better.

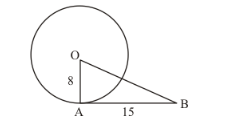
Since the tangent will always be perpendicular to the radius we have drawn OA perpendicular to AB. To find the length of OB we have to use Pythagoras theorem.

$O B^{2}=O A^{2}+A B^{2}$

$O B^{2}=8^{2}+15^{2}$

$O B^{2}=64+225$

$O B^{2}=289$

$O B=\sqrt{289}$

$O B=17$

Therefore, length of OB is 17 cm.