O is the circumcentre of the ΔABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
Thinking Process
Firstly, prove that ΔBOD and ΔCOD are congruent by SSS rule. Further, use the theorem that in a circle, the angle subtended by an arc at the centre
is twice the angle subtended by it at the remaining part of the circle and prove the required result.
Given In a ΔABC a circle is circumscribed having centre O.
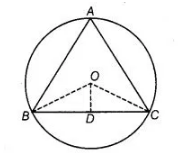
Also, $D$ is the mid-point of $B C$.
To prove $\angle B O D=\angle A$ or $\angle B O D=\angle B A C$
Construction Join $O B, O D$ and $O C$.
Proof in $\triangle B O D$ and $\triangle C O D$,
$O B=O C$ [both are the radius of circle]
$B D=D C$ [ $D$ is the mid-point of $B C$ ]
and $O D=O D$ [common side]
$\therefore$ $\triangle B O D \cong \triangle C O D$ [by SSS congruence rule]
$\therefore$ $\angle B O D=\angle C O D$ [by CPCT] ...(i)
We know that, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.
$\therefore \quad 2 \angle B A C=\angle B O C$
$\angle B A C=\frac{2}{2} \angle B O D$ $[\because \angle B O C=2 \angle B O D]$ [from Eq. (i)]
$\Rightarrow \quad \angle B A C=\angle B O D$
Hence proved.