Question:
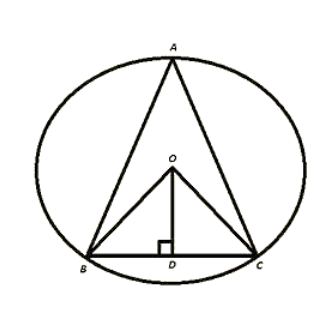
O is the circumference of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A.
Solution:
Given O is the circum centre of triangle ABC and OD⊥BC
To prove ∠BOD = 2∠A
Proof:
In ΔOBD and ΔOCD
∠ODB = ∠ODC [Each 90°]
OB = OC [Radius of circle]
OD = OD [Common]
Then ΔOBD ≅ ΔOCD [By RHS Condition].
∴ ∠BOD = ∠COD .... (i) [PCT].
By degree measure theorem
∠BOC = 2∠BAC
⇒ 2∠BOD = 2∠BAC [By using (i)]
⇒ ∠BOD = ∠BAC.
