Question:
O is the origin and A is (a, b, c). Find the direction cosines of the line OA and the equation of plane through A at right angle to OA.
Solution:
Given, O (0, 0, 0) and A(a, b, c)
So, the direction ratios of OA = a – 0, b – 0, c – 0 = a, b, c
And, the direction cosines of line OA
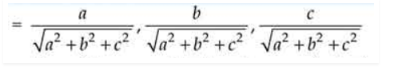
Now, the direction ratios of the normal to the plane are (a, b, c).
We know that, the equation of the plan passing through the point A(a, b, c) is
a(x – a) + b(y – b) + c(z – c) = 0
ax – a2 + by – b2 + cz – c2 = 0
ax + by + cz = a2 + b2 + c2
Thus, the required equation of the plane is ax + by + cz = a2 + b2 + c2
