Obtain the maximum kinetic energy of β-particles,

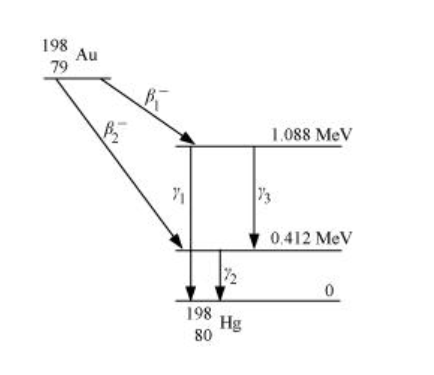
It can be observed from the given γ-decay diagram that γ1 decays from the 1.088 MeV energy level to the 0 MeV energy level.

Hence, the energy corresponding to γ1-decay is given as:

E1 = 1.088 − 0 = 1.088 MeV

hν1= 1.088 × 1.6 × 10−19 × 106 J

Where,

h = Planck’s constant = 6.6 × 10−34 Js

ν1 = Frequency of radiation radiated by γ1-decay

$\therefore v_{1}=\frac{E_{1}}{h}$

$=\frac{1.088 \times 1.6 \times 10^{-19} \times 10^{6}}{6.6 \times 10^{-34}}=2.637 \times 10^{20} \mathrm{~Hz}$

It can be observed from the given γ-decay diagram that γ2 decays from the 0.412 MeV energy level to the 0 MeV energy level.

Hence, the energy corresponding to γ2-decay is given as:

E2 = 0.412 − 0 = 0.412 MeV

hν2= 0.412 × 1.6 × 10−19 × 106 J

Where,

ν2 = Frequency of radiation radiated by γ2-decay

$\therefore v_{2}=\frac{E_{2}}{h}$

$=\frac{0.412 \times 1.6 \times 10^{-19} \times 10^{6}}{6.6 \times 10^{-34}}=9.988 \times 10^{19} \mathrm{~Hz}$

It can be observed from the given γ-decay diagram that γ3 decays from the 1.088 MeV energy level to the 0.412 MeV energy level.

Hence, the energy corresponding to γ3-decay is given as:

E3 = 1.088 − 0.412 = 0.676 MeV

hν3= 0.676 × 10−19 × 106 J

Where,

ν3 = Frequency of radiation radiated by γ3-decay

$\therefore v_{3}=\frac{E_{3}}{h}$

$=\frac{0.676 \times 1.6 \times 10^{-19} \times 10^{6}}{6.6 \times 10^{-34}}=1.639 \times 10^{20} \mathrm{~Hz}$

Mass of $m\left({ }_{78}^{198} \mathrm{Au}\right)=197.968233 \mathrm{u}$

Mass of $m\left({ }_{80}^{198} \mathrm{Hg}\right)=197.966760 \mathrm{u}$

1 u = 931.5 MeV/c2

Energy of the highest level is given as:

$E=\left[m\left({ }_{78}^{198} \mathrm{Au}\right)-m\left({ }_{80}^{190} \mathrm{Hg}\right)\right]$

$=197.968233-197.966760=0.001473 \mathrm{u}$

$=0.001473 \times 931.5=1.3720995 \mathrm{MeV}$

β1 decays from the 1.3720995 MeV level to the 1.088 MeV level

∴Maximum kinetic energy of the β1 particle = 1.3720995 − 1.088

= 0.2840995 MeV

β2 decays from the 1.3720995 MeV level to the 0.412 MeV level

∴Maximum kinetic energy of the β2 particle = 1.3720995 − 0.412

= 0.9600995 MeV