On a horizontal plane there is vertical tower with a flag pole on the top of the tower.

Let AB be the tower of height h and AD be the flag pole on tower. At the point 9m away from the foot of tower, the angle of elevation of the top and bottom of flag pole are 60° and 30°. Let AD = x, BC = 9 and, .

Here we have to find height of tower and height of flag pole.

The corresponding diagram is as follows

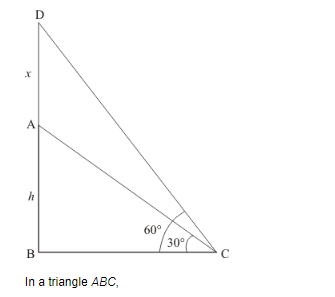
$\Rightarrow \quad \tan C=\frac{A B}{B C}$

$\Rightarrow \quad \tan 30^{\circ}=\frac{h}{9}$

$\Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{h}{9}$

$\Rightarrow \quad h=\frac{9}{\sqrt{3}}$

$\Rightarrow h=3 \sqrt{3}$

Again in a triangle,

$\Rightarrow \quad \tan C=\frac{A D+A B}{B C}$

$\Rightarrow \tan 60^{\circ}=\frac{h+x}{9}$

$\Rightarrow \quad \sqrt{3}=\frac{h+x}{9}$

$\Rightarrow \quad 9 \sqrt{3}=h+x$

$\Rightarrow \quad 9 \sqrt{3}=3 \sqrt{3}+x$

$\Rightarrow \quad x=6 \sqrt{3}$

So height of tower is $3 \sqrt{3}$ meter and height of flag pole is $6 \sqrt{3}$ meters.