One man is sitting on the shores of a river. He is in the line of $1.0 \mathrm{~m}$ long boat and is $5.5 \mathrm{~m}$ away from the center of the boat. If he can throw the apply only with a speed of $10 \mathrm{~m} / \mathrm{s}$. find the minimum and maximum angles of projection for successful shot. Assume that the point of projection and the edge pf the boat are in the same horizontal level.
For near point of boat
$\mathrm{R}=5 \mathrm{~m}=\frac{\mathrm{u}^{\mathrm{m}} \sin 2 \theta}{\mathrm{g}} \mathrm{g}$
$5=\frac{(10)^{2} \sin 2 e}{g}$
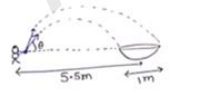
$\theta=15^{\circ}$ or $75^{\circ}$
For for point of boat
$\mathrm{R}=6 \mathrm{~m}=\frac{\mathrm{u}^{\mathrm{a}^{\mathrm{s}} \sin 2 \theta}}{\mathrm{g}}$
$\theta=18^{\circ}$ or $71^{\circ}$
For a successful shot angle may vary from $15^{\circ}$ to $18^{\circ}$ or $71^{\circ}$ to $75^{\circ}$
Minimum angle $=15^{\circ}$
Maximum angle $=75^{\circ}$
