P (a, b) is the mid-point of a line segment between axes.

Solution:

Let AB be the line segment between the axes and let P (a, b) be its mid-point.

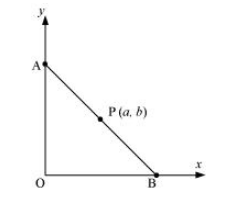
Let the coordinates of A and B be (0, y) and (x, 0) respectively.

Since P (a, b) is the mid-point of AB,

$\left(\frac{0+x}{2}, \frac{y+0}{2}\right)=(a, b)$

$\Rightarrow\left(\frac{x}{2}, \frac{y}{2}\right)=(a, b)$

$\Rightarrow \frac{x}{2}=a$ and $\frac{y}{2}=b$

$\therefore x=2 a$ and $y=2 b$

Thus, the respective coordinates of A and B are (0, 2b) and (2a, 0).

The equation of the line passing through points (0, 2b) and (2a, 0) is

$(y-2 b)=\frac{(0-2 b)}{(2 a-0)}(x-0)$

$y-2 b=\frac{-2 b}{2 a}(x)$

$a(y-2 b)=-b x$

i.e., $b x+a y=2 a b$

On dividing both sides by ab, we obtain

$\frac{b x}{a b}+\frac{a y}{a b}=\frac{2 a b}{a b}$

$\Rightarrow \frac{x}{a}+\frac{y}{b}=2$

Thus, the equation of the line is $\frac{x}{a}+\frac{y}{b}=2$.