Particle $A$ of mass $m_{A}=\frac{m}{2}$ moving along the $x$-axis with velocity $v_{0}$ collides elastically with another particle $B$ at
rest having mass $m_{B}=\frac{m}{3}$. If both particles move along
the $x$-axis after the collision, the change $\Delta \lambda$ in de-Broglie wavelength of particle $A$, in terms of its de-Broglie wavelength $\left(\lambda_{0}\right)$ before collision is :
Correct Option: , 4
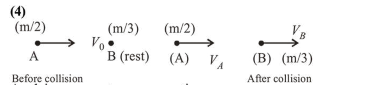
Applying momentum conservation
$\frac{m}{2} \times V_{0}+\frac{m}{3} \times(0)=\frac{m}{2} V_{A}+\frac{m}{3} V_{B}$
$=\frac{V_{0}}{2}=\frac{V_{A}}{2}+\frac{V_{B}}{3}$ ...(1)
Since, collision is elastic
$e=1=\frac{V_{B}-V_{A}}{V_{0}} \Rightarrow V_{0}=V_{B}-V_{A}$ ...(2)
On solving equations (i) and (ii) $: V_{A}=\frac{V_{0}}{5}$
Now, de-Broglie wavelength of $A$ before collision :
$\lambda_{0}=\frac{h}{m_{A} V_{0}}=\frac{h}{\left(\frac{m}{2}\right) V_{0}} \Rightarrow \lambda_{0}=\frac{2 h}{m V_{0}}$
Final de-Broglie wavelength :
$\lambda_{f}=\frac{h}{m_{A} V_{0}}=\frac{h}{\frac{m}{2} \times \frac{V_{0}}{5}} \Rightarrow \lambda_{f}=\frac{10 h}{m V_{0}}$
$\therefore \Delta \lambda=\lambda_{f}-\lambda_{0}=\frac{10 h}{m V_{0}}-\frac{2 h}{m V_{0}}$
$\Rightarrow \Delta \lambda=\frac{8 h}{m v_{0}} \Rightarrow \Delta \lambda=4 \times \frac{2 h}{m v_{0}}$
$\therefore \Delta \lambda=4 \lambda_{0}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.