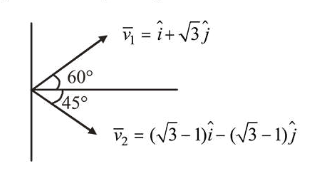Particle $A$ of mass $m_{1}$ moving with velocity $(\sqrt{3} \hat{i}+\hat{j}) \mathrm{ms}^{-1}$ collides with another particle $\mathrm{B}$ of mass $\mathrm{m}_{2}$ which is at rest initially. Let $\vec{V}_{1}$ and $\vec{V}_{2}$ be the velocities of particles A and $\mathrm{B}$ after collision respectively. If $\mathrm{m}_{1}=2 \mathrm{~m}_{2}$ and after collision $\overrightarrow{\mathrm{V}}_{1}=(\hat{i}+\sqrt{3} \hat{j}) \mathrm{ms}^{-1}$, the angle between $\overrightarrow{\mathrm{V}}_{1}$ and $\overrightarrow{\mathrm{V}}_{2}$ is :
Correct Option: , 4
(4) Before collision,
Velocity of particle $A, u_{1}=(\sqrt{3} \hat{i}+\hat{j}) \mathrm{m} / \mathrm{s}$
Velocity of particle $B, u_{2}=0$
After collision,
Velocity of particle $A, v_{1}=(\hat{i}+\sqrt{3} \hat{j})$
Velocity of particle $B, v_{2}=0$
Using principal of conservation of angular momentum
$m_{1} \vec{u}_{1}+m_{2} \vec{u}_{2}=m_{1} \vec{v}_{1}+m_{2} \vec{v}_{2}$
$\Rightarrow 2 m_{2}(\sqrt{3} \hat{i}+\hat{j})+m_{2} \times 0=2 m_{2}(\hat{i}+\sqrt{3} \hat{j})+m_{2} \times \vec{v}_{2}$
$\Rightarrow 2 \sqrt{3} \hat{i}+2 \hat{j}=2 \hat{i}+2 \sqrt{3} \hat{j}+\vec{v}_{2}$
$\Rightarrow \vec{v}_{2}=(\sqrt{3}-1) \hat{i}-(\sqrt{3}-1) \hat{j} \Rightarrow \vec{v}_{1}=\hat{i}+\sqrt{3} \hat{j}$
For angle between $\vec{v}_{1}$ and $\vec{v}_{2}$,
$\cos \theta=\frac{\vec{v}_{1} \cdot \vec{v}_{2}}{\vec{v}_{1} \vec{v}_{2}}=\frac{2(\sqrt{3}-1)(1-\sqrt{3})}{2 \times 2 \sqrt{2}(\sqrt{3}-1)}=\frac{1-\sqrt{3}}{2 \sqrt{2}}$
$\Rightarrow \theta=105^{\circ}$
Angle between $\vec{v}_{1}$ and $\vec{v}_{2}$ is $105^{\circ}$