Prove that

Solution:

$\left(x^{3}-3 x y^{2}\right) d x=\left(y^{3}-3 x^{2} y\right) d y$

$\Rightarrow \frac{d y}{d x}=\frac{x^{3}-3 x y^{2}}{y^{3}-3 x^{2} y}$                $\ldots(1)$

This is a homogeneous equation. To simplify it, we need to make the substitution as:

$y=v x$

$\Rightarrow \frac{d}{d x}(y)=\frac{d}{d x}(v x)$

$\Rightarrow \frac{d y}{d x}=v+x \frac{d v}{d x}$

Substituting the values of $y$ and $\frac{d v}{d x}$ in equation (1), we get:

$v+x \frac{d v}{d x}=\frac{x^{3}-3 x(v x)^{2}}{(v x)^{3}-3 x^{2}(v x)}$

$\Rightarrow v+x \frac{d v}{d x}=\frac{1-3 v^{2}}{v^{3}-3 v}$

$\Rightarrow x \frac{d v}{d x}=\frac{1-3 v^{2}}{v^{3}-3 v}-v$

$\Rightarrow x \frac{d v}{d x}=\frac{1-3 v^{2}-v\left(v^{3}-3 v\right)}{v^{3}-3 v}$

$\Rightarrow x \frac{d v}{d x}=\frac{1-v^{4}}{v^{3}-3 v}$

$\Rightarrow\left(\frac{v^{3}-3 v}{1-v^{4}}\right) d v=\frac{d x}{x}$

Integrating both sides, we get:

$\int\left(\frac{v^{3}-3 v}{1-v^{4}}\right) d v=\log x+\log C^{\prime}$                  ...(2)

Now, $\int\left(\frac{v^{3}-3 v}{1-v^{4}}\right) d v=\int \frac{v^{3} d v}{1-v^{4}}-3 \int \frac{v d v}{1-v^{4}}$

$\Rightarrow \int\left(\frac{v^{3}-3 v}{1-v^{4}}\right) d v=I_{1}-3 I_{2}$, where $I_{1}=\int \frac{v^{3} d v}{1-v^{4}}$ and $I_{2}=\int \frac{v d v}{1-v^{4}}$      ...(3)

Let $1-v^{4}=t$

$\therefore \frac{d}{d v}\left(1-v^{4}\right)=\frac{d t}{d v}$

$\Rightarrow-4 v^{3}=\frac{d t}{d v}$

$\Rightarrow v^{3} d v=-\frac{d t}{4}$

Now, $I_{1}=\int \frac{-d t}{4 t}=-\frac{1}{4} \log t=-\frac{1}{4} \log \left(1-v^{4}\right)$

And, $I_{2}=\int \frac{v d v}{1-v^{4}}=\int \frac{v d v}{1-\left(v^{2}\right)^{2}}$

Let $v^{2}=p$

$\therefore \frac{d}{d v}\left(v^{2}\right)=\frac{d p}{d v}$

$\Rightarrow 2 v=\frac{d p}{d v}$

$\Rightarrow v d v=\frac{d p}{2}$

$\Rightarrow I_{2}=\frac{1}{2} \int \frac{d p}{1-p^{2}}=\frac{1}{2 \times 2} \log \left|\frac{1+p}{1-p}\right|=\frac{1}{4} \log \left|\frac{1+v^{2}}{1-v^{2}}\right|$

Substituting the values of I1 and I2 in equation (3), we get:

$\int\left(\frac{v^{3}-3 v}{1-v^{4}}\right) d v=-\frac{1}{4} \log \left(1-v^{4}\right)-\frac{3}{4} \log \left|\frac{1-v^{2}}{1+v^{2}}\right|$

Therefore, equation (2) becomes:

$\frac{1}{4} \log \left(1-v^{4}\right)-\frac{3}{4} \log \left|\frac{1+v^{2}}{1-v^{2}}\right|=\log x+\log \mathrm{C}^{\prime}$

$\Rightarrow-\frac{1}{4} \log \left[\left(1-v^{4}\right)\left(\frac{1+v^{2}}{1-v^{2}}\right)^{3}\right]=\log \mathrm{C}^{\prime} x$

$\Rightarrow \frac{\left(1+v^{2}\right)^{4}}{\left(1-v^{2}\right)^{2}}=\left(\mathrm{C}^{\prime} x\right)^{-4}$

$\Rightarrow \frac{\left(1+\frac{y^{2}}{x^{2}}\right)^{4}}{\left(1-\frac{y^{2}}{x^{2}}\right)^{2}}=\frac{1}{\mathrm{C}^{\prime 4} x^{4}}$

$\Rightarrow \frac{\left(x^{2}+y^{2}\right)^{4}}{x^{4}\left(x^{2}-y^{2}\right)^{2}}=\frac{1}{\mathrm{C}^{44} x^{4}}$

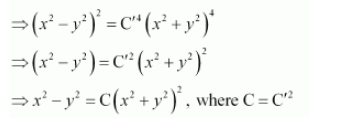
Hence, the given result is proved.